
위상 정렬?
순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘이다. 이론적으로는 비순환 방향 그래프(DAG, Direct Acyclic Graph)에서 그래프의 방향성을 거르지 않고 정점들을 나열하는 알고리즘이다.
예를 들어 A작업이 끝난 후 B작업을 실행할 수 있고, C작업이 끝난 후 B작업을 실행할 수 있다고 할때 작업의 순서는 ACB 또는 CAB가 될 수 있다. 이렇게 정해진 순서를 위배하지 않으면서 모든 정점을 나열하는 알고리즘을 위상 정렬이라고 한다. 일반적으로 위상 정렬의 결과는 유일하지 않다.
동작 과정
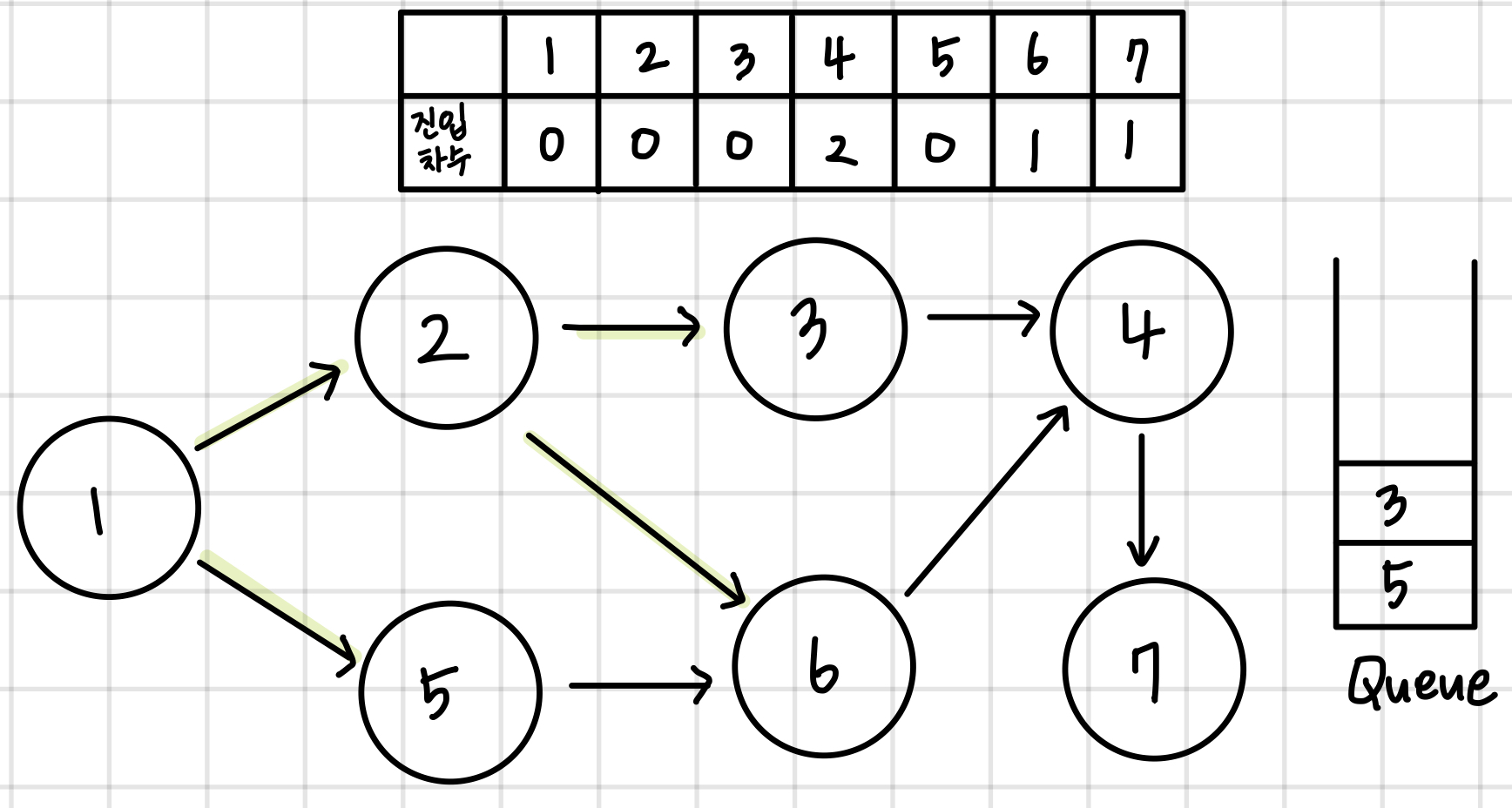
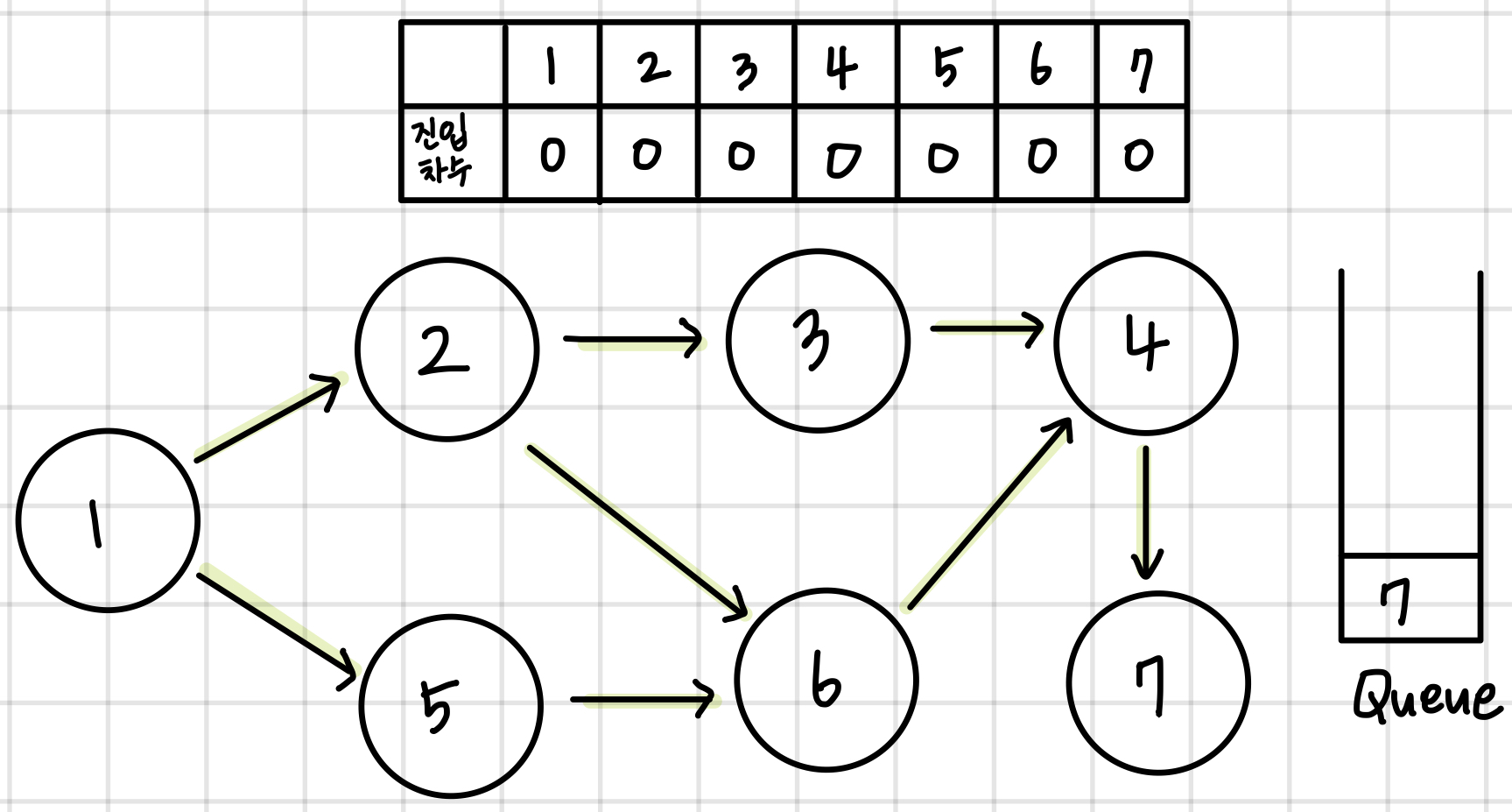
배열에 각 노드들의 진입 차수를 저장한다. queue에는 진입차수가 0인 모든 노드들이 삽입된다.

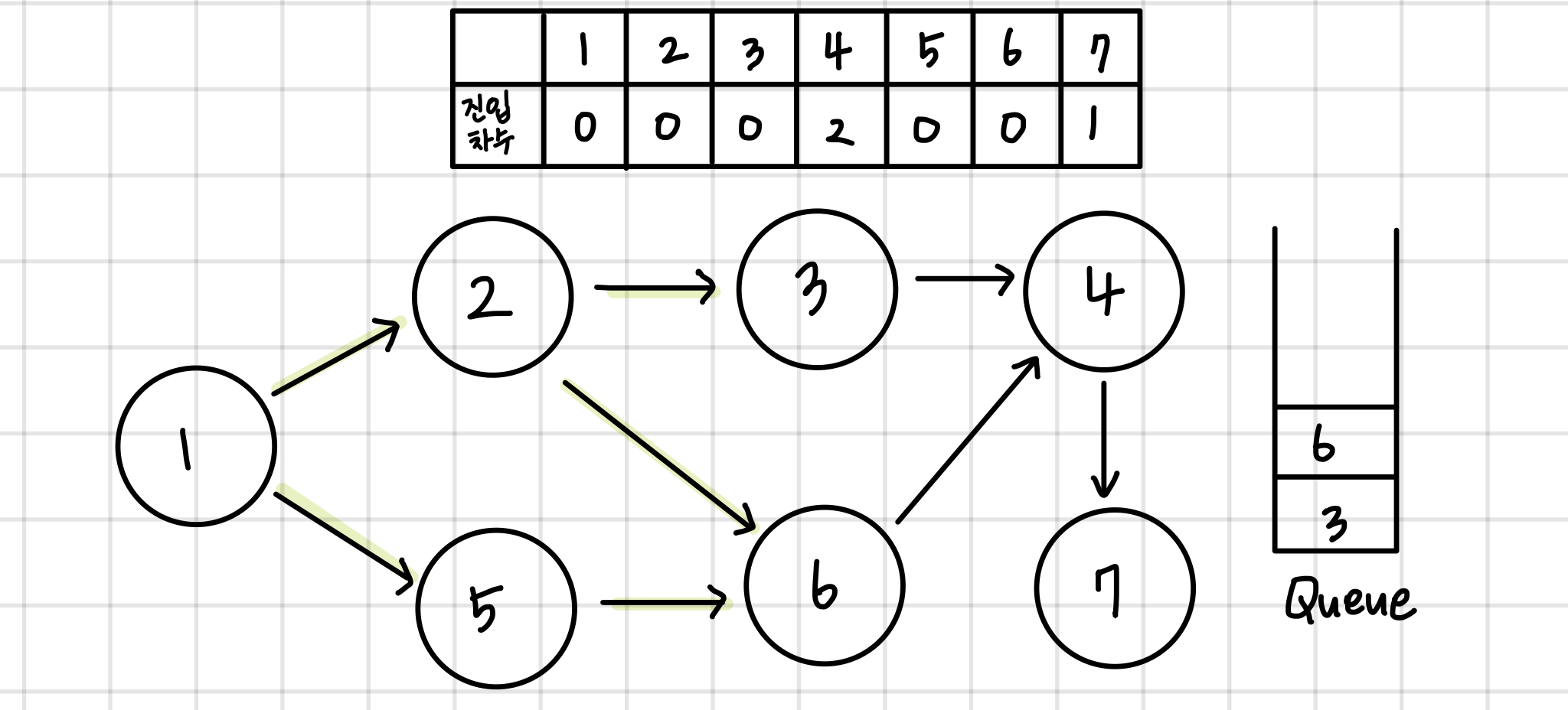
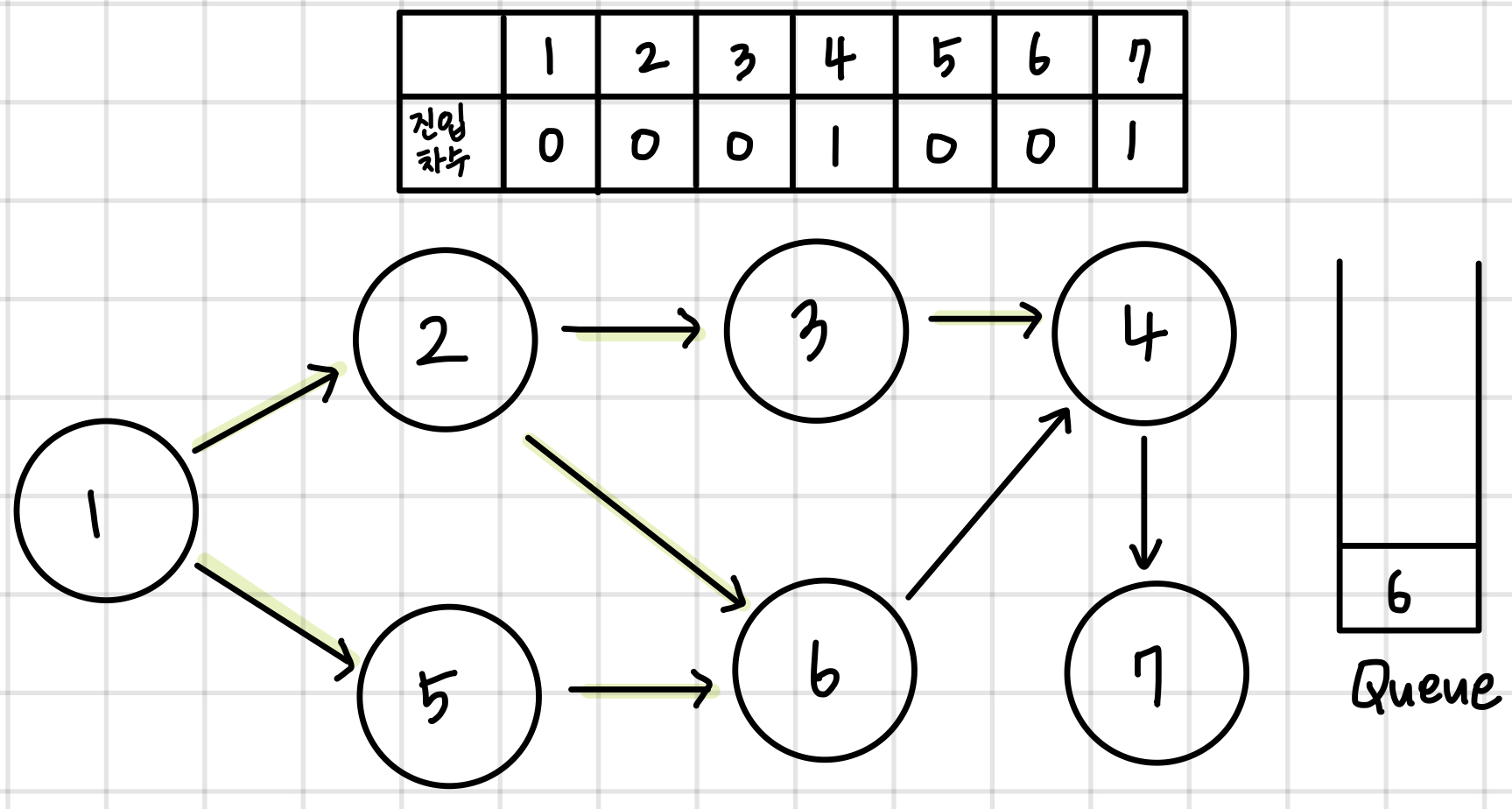
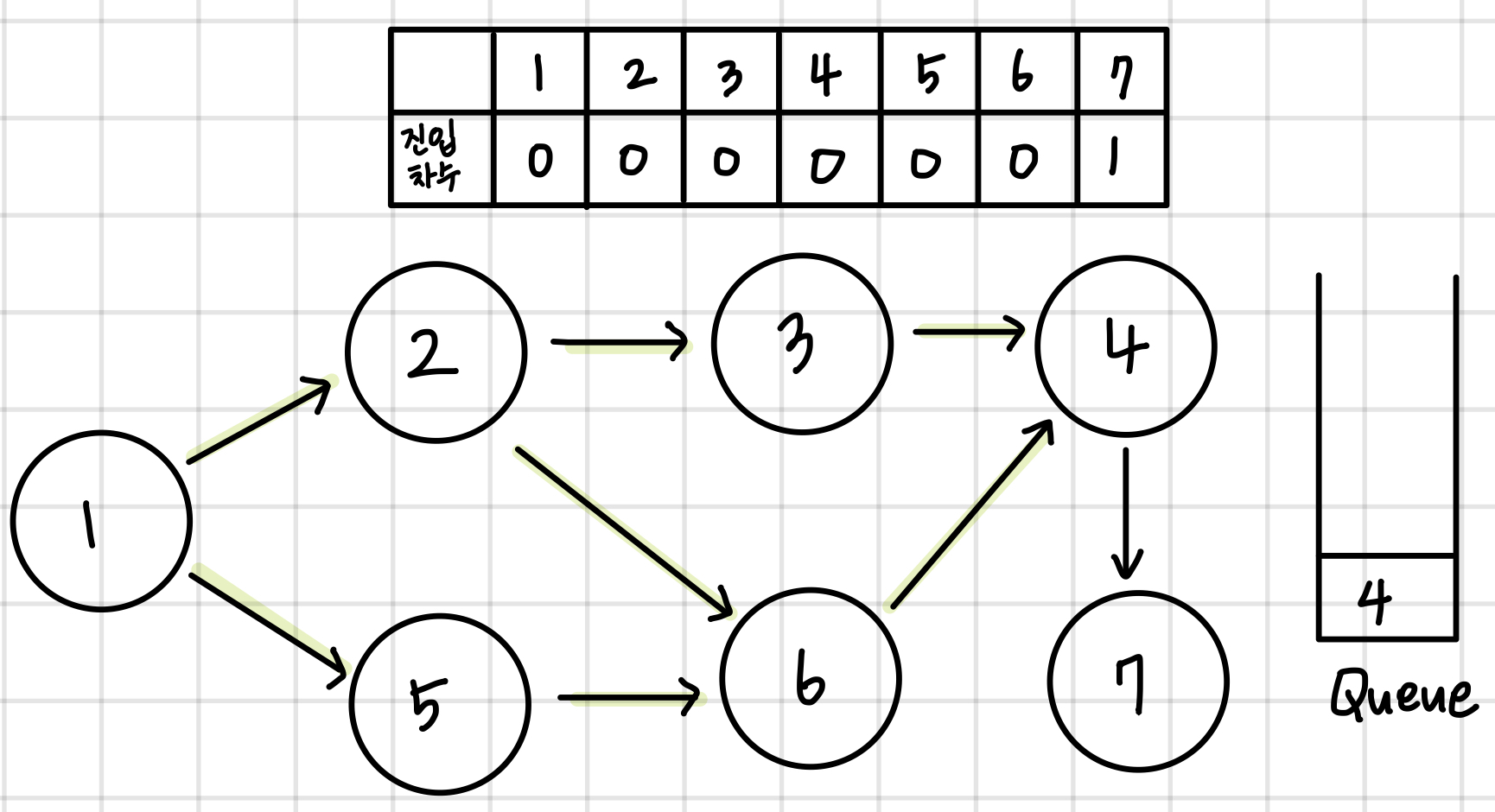
queue의 첫번째 값을 꺼낸다. 이 노드에 연결된 모든 간선들을 제거한다. 이후 진입차수가 0인 모든 노드들을 queue에 넣어준다.

queue가 빌때까지 이 과정을 반복한다. 결과적으로 queue에서 pop되는 노드들의 순서가 구하고자 하는 답이 된다.
1 -> 2 -> 5 -> 3 -> 6 -> 4 -> 7
코드 (c++)
초기화
for (int i = 0; i < m; i++) { int a, b; cin >> a >> b; // a -> b node[a].push_back(b); indegree[b]++; } for (int i = 1; i <= n; i++) { if (indegree[i] == 0) q.push(i); }
인접 리스트를 통해 연결된 노드들을 기록하고, 진입 차수를 기록한다. 이후 진입 차수가 0인 노드들을 queue에 저장한다.
while (!q.empty()) { int cur = q.front(); cout<<cur<<" "; q.pop(); for (int i = 0; i < node[cur].size(); i++) { int nextNode = node[cur][i]; indegree[nextNode]--; if (indegree[nextNode] == 0) q.push(nextNode); } }
queue에서 첫번째 노드를 pop해주고 이 노드와 연결된 노드들을 방문하며 간선들을 제거한다. 이때 진입 차수가 0이 되는 노드들은 queue에 저장한다. queue가 빌때까지 이 과정을 반복한다.
예제
https://www.acmicpc.net/problem/2252
2252번: 줄 세우기
첫째 줄에 N(1 ≤ N ≤ 32,000), M(1 ≤ M ≤ 100,000)이 주어진다. M은 키를 비교한 회수이다. 다음 M개의 줄에는 키를 비교한 두 학생의 번호 A, B가 주어진다. 이는 학생 A가 학생 B의 앞에 서야 한다는 의
www.acmicpc.net
'알고리즘 > 공부' 카테고리의 다른 글
| Javascript로 백준 풀기 (4) | 2023.03.13 |
|---|---|
| [알고리즘] 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2022.01.12 |
| [알고리즘] 유니언 파인드(Union Find) (0) | 2022.01.10 |
| [알고리즘] 인덱스 트리(Indexed Tree) (1) | 2022.01.05 |
| [알고리즘] 그래프 (0) | 2021.09.20 |