
인덱스 트리란?
포화 이진 트리 형태의 자료구조로 부모 노드가 자식 노드의 대표값을 가지는 트리이다. 리프 노드에 사용할 값들을 적어놓고, 부모 노드에 값들의 합을 모아놓은 형태이다. 글보다 아래 그림 예제를 보면 쉽게 이해할 수 있다.

언제 사용?
배열 A가 있고 아래 두 연산을 M번 수행해야 하는 문제가 있다고 하자.
1️⃣ 구간 l, r이 주어졌을 때 A[l]+A[l+1]+...+A[r-1]+A[r]을 구해라
2️⃣ i번째 수 A[i]를 X로 바꾸어라
N개의 수가 있다고 할 때 일반적인 방법으로는 1번 연산을 수행하는데는 O(N), 2번 연산을 수행하는 데에는 O(1)이 걸려 결과적으로 시간 복잡도는 O(NM)이 된다. 누적합 배열을 사용해서 풀게 되어도 1번 연산 O(1), 2번연산 O(N)으로 O(NM)의 시간 복잡도를 가진다. 하지만 인덱스 트리를 사용한다면 1번 연산 O(logN) 2번 연산 O(logN)으로 두 연산을 O(MlogN)에 수행할 수 있게 된다.
결론적으로 값이 변하는 구간합을 여러번 구해야 할 때 사용하면 좋다.
Bottom Up, Top Down 모두 사용할 수 있지만 재귀를 사용하고 싶지 않기때문에 Bottom Up 방식으로 진행해보도록 하겠다. 만약 2~4의 구간 합을 구하고자 하면 아래 그림과 같다.

코드 (C++)
초기화
이진 트리를 일차원 배열을 이용하여 구현해보자. 계산의 편리함을 위해 루트 노드의 인덱스는 1로 설정해준다. 왼쪽 child는 index*2, 오른쪽 child는 index*2+1의 인덱스 값을 가지게 된다.
구해야 하는 값들의 개수가 N개라면 이 값을 넘는 2m으로 노드의 개수를 설정해준다. 예를들어 N이 6이라면 이 값을 만족하는 m은 3으로 리프 노드는 8개가 되게 된다. 이 값은 리프 노드의 가장 첫번째 값의 인덱스 값이 된다. 이 값을 통해 트리의 크기(배열의 크기) 2m∗2도 구할 수 있다.
int temp = 1; while(temp<=N) temp*=2; for(int i=0; i<A.length(); i++){ tree[temp+i] = A[i]; }
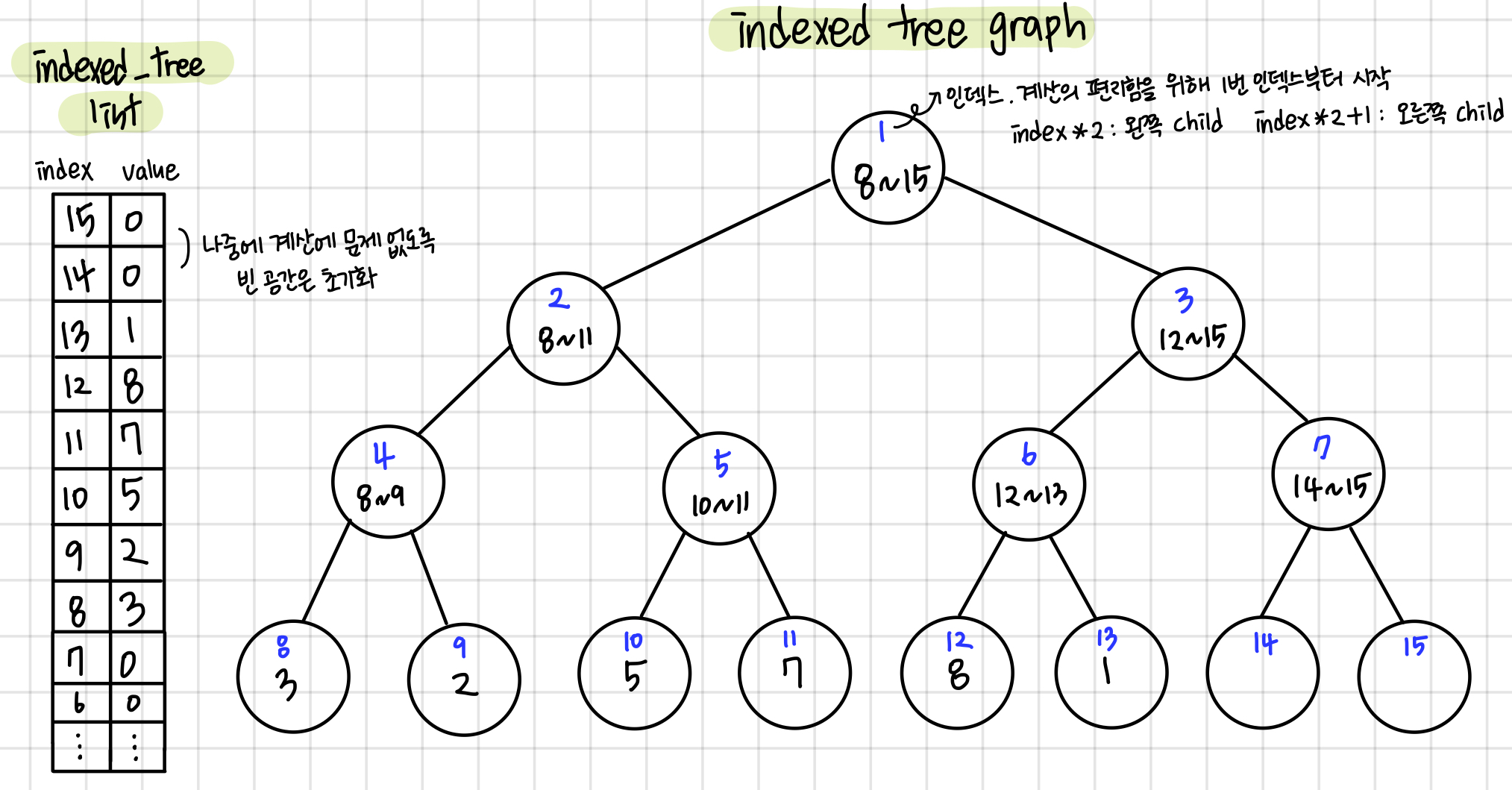
리프 노드에 값을 업데이트 했다면 tree[parent] = tree[left_child]+tree[right_child]를 통해 나머지 노드 값들을 구할 수 있다.
// startIndex는 리프 노드의 첫번째 인덱스 for (int i = startIndex - 1; i > 0; i--) { tree[i] = tree[2 * i] + tree[2 * i + 1]; }
값 업데이트
위의 예시에서 4번째 수 7을 9로 업데이트한다고 하자. 관련 노드는 아래 그림에서 파란색으로 색칠한 노드들이 된다. 값이 변경된 차만큼 연관 노드들을 업데이트해주면 된다. 여기서 관련 노드는 parent 노드로 나누기 2를 통해 쉽게 구할 수 있다.
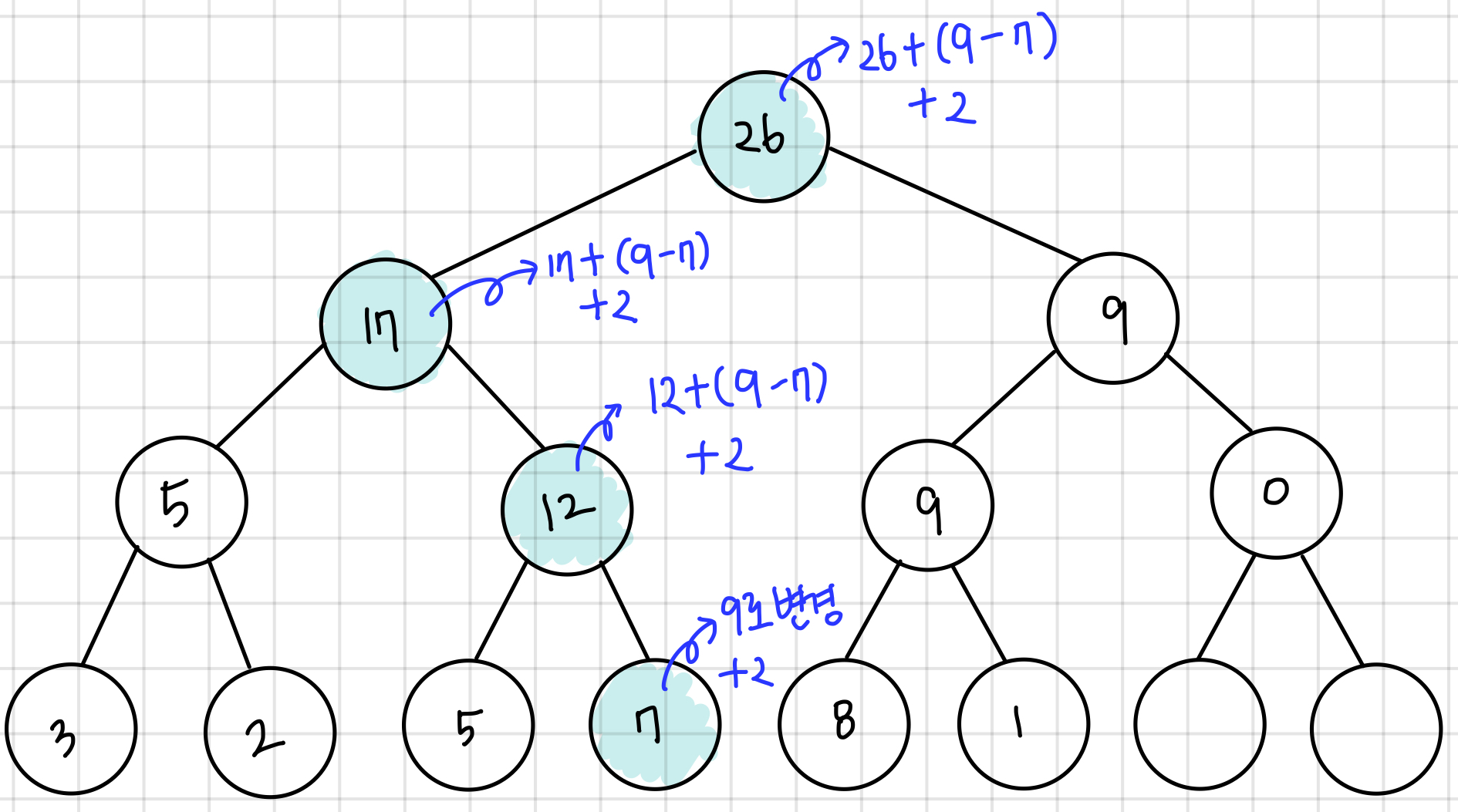
b번째 값을 c로 변경하는 코드는 아래와 같다.
void update(int index, int value) { while (index > 0) { tree[index] += value; index /= 2; } } update(b + startIndex - 1, c-tree[b + startIndex - 1])
구간 합 구하기
글보다는 그림과 코드를 보며 이해하는 것이 편하다. 그림에서 파란색으로 칠한 노드값들을 더하면 구하고자 하는 구간 합을 구할 수 있다.
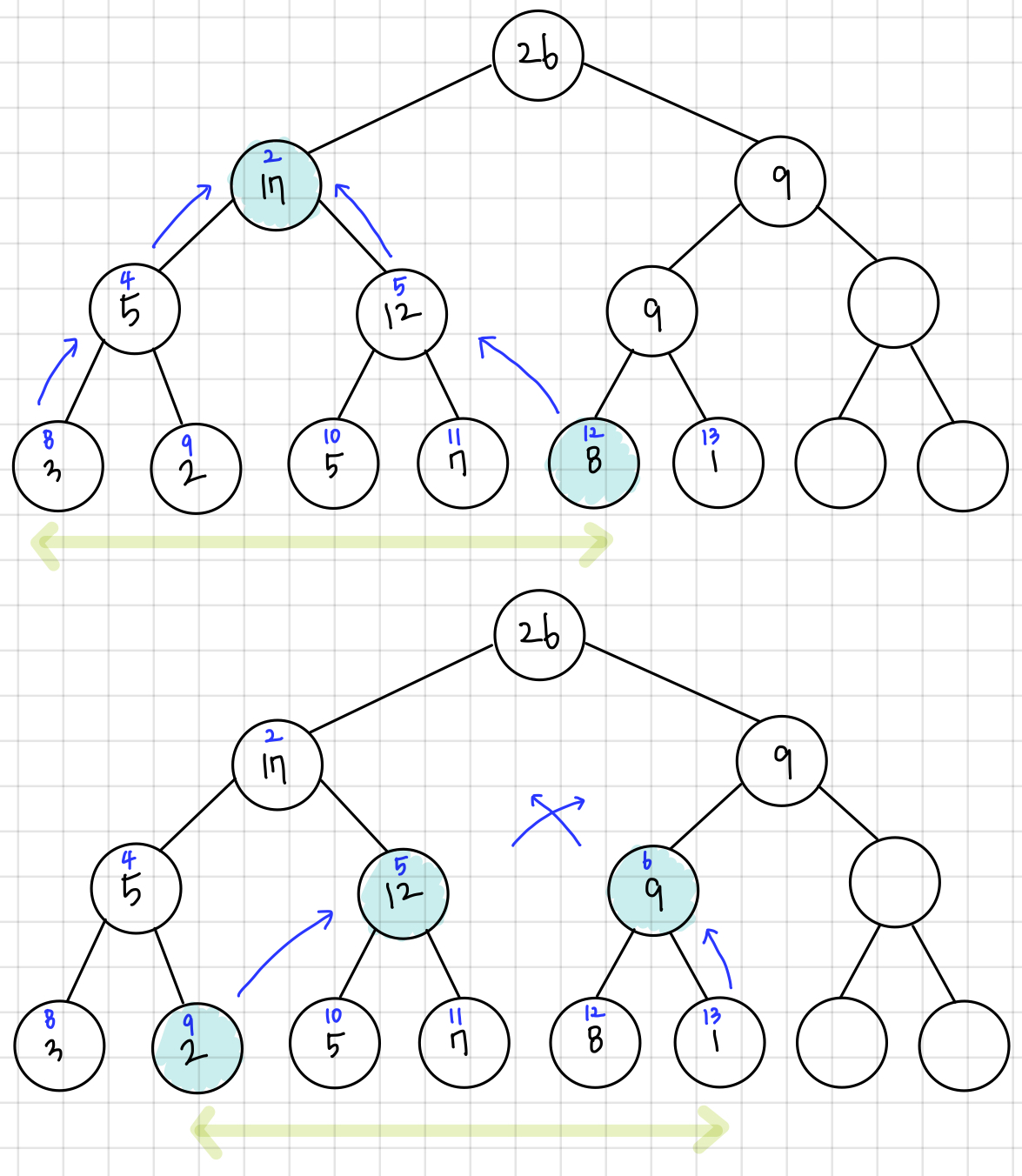
b부터 c까지의 구간합을 구하는 코드는 아래와 같다
int getSum(int left, int right) { int ans = 0; while (left <= right) { if (left % 2 == 1) { ans += tree[left]; } if (right % 2 == 0) { ans += tree[right]; } left = (left + 1) / 2; right = (right - 1) / 2; } return ans; } getSum(b + startIndex - 1, c + startIndex - 1)
예제/문제
https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
'알고리즘 > 공부' 카테고리의 다른 글
| [알고리즘] 위상정렬(Topological Sort) (0) | 2022.01.11 |
|---|---|
| [알고리즘] 유니언 파인드(Union Find) (0) | 2022.01.10 |
| [알고리즘] 그래프 (0) | 2021.09.20 |
| [알고리즘] 다이나믹 프로그래밍(동적 계획법) (0) | 2021.09.20 |
| [알고리즘] 수학 (0) | 2021.09.20 |