
다익스트라 알고리즘?
한 정점에서 다른 정점까지의 최단경로를 구하는 알고리즘이다. 각 정점을 최대 한번씩만 방문하여 최단 거리를 정한다. 시작 노드로부터 각 노드까지의 거리를 저장하는 배열을 이용하여 탐색을 진행하면서 현재 누적 최단 거리와 간선의 가중치의 합이 이동하는 노드까지의 저장된 최단 거리보다 작을 경우 값을 업데이트해주며 구하고자 하는 바를 구한다. 다익스트라는 모든 가중치가 음이 아닐때만 사용할 수 있다.
동작 과정
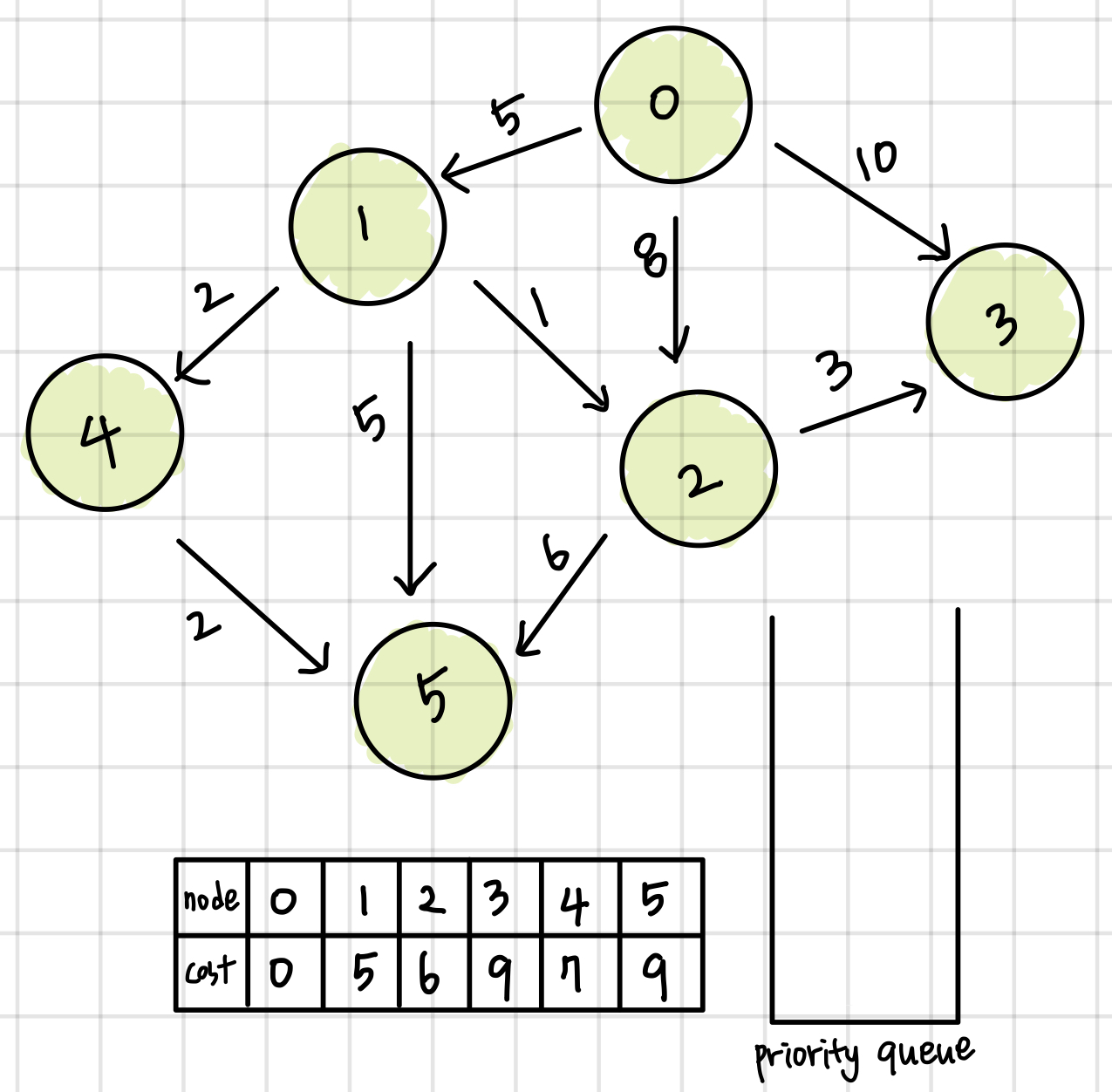
아래 그림과 같은 예시에서 0번 노드에서 5번 노드로 가는 최단경로를 구하고 한다고 해보자. 최단거리를 저장하는 배열을 모두 INF로 설정해준다. priority queue에는 (노드, 누적거리)를 저장한다. 이 priority queue는 누적 거리를 기준으로 오름차순으로 정렬되도록한다.

0번 노드를 방문하고 0번 노드에서 갈 수 있는 노드들(연결되어있고 아직 방문하지 않은 노드)을 선택한다. 만약 누적거리+가중치가 cost배열값보다 작다면 이를 업데이트 해준다. 값을 업데이트 해주었다면 이를 priority queue에 저장한다.

큐에 저장되어있는 가장 front 값인 1번 노드를 방문한다. 1번 노드에서 갈 수 있는 노드들을 확인하며 값을 업데이트해준다.
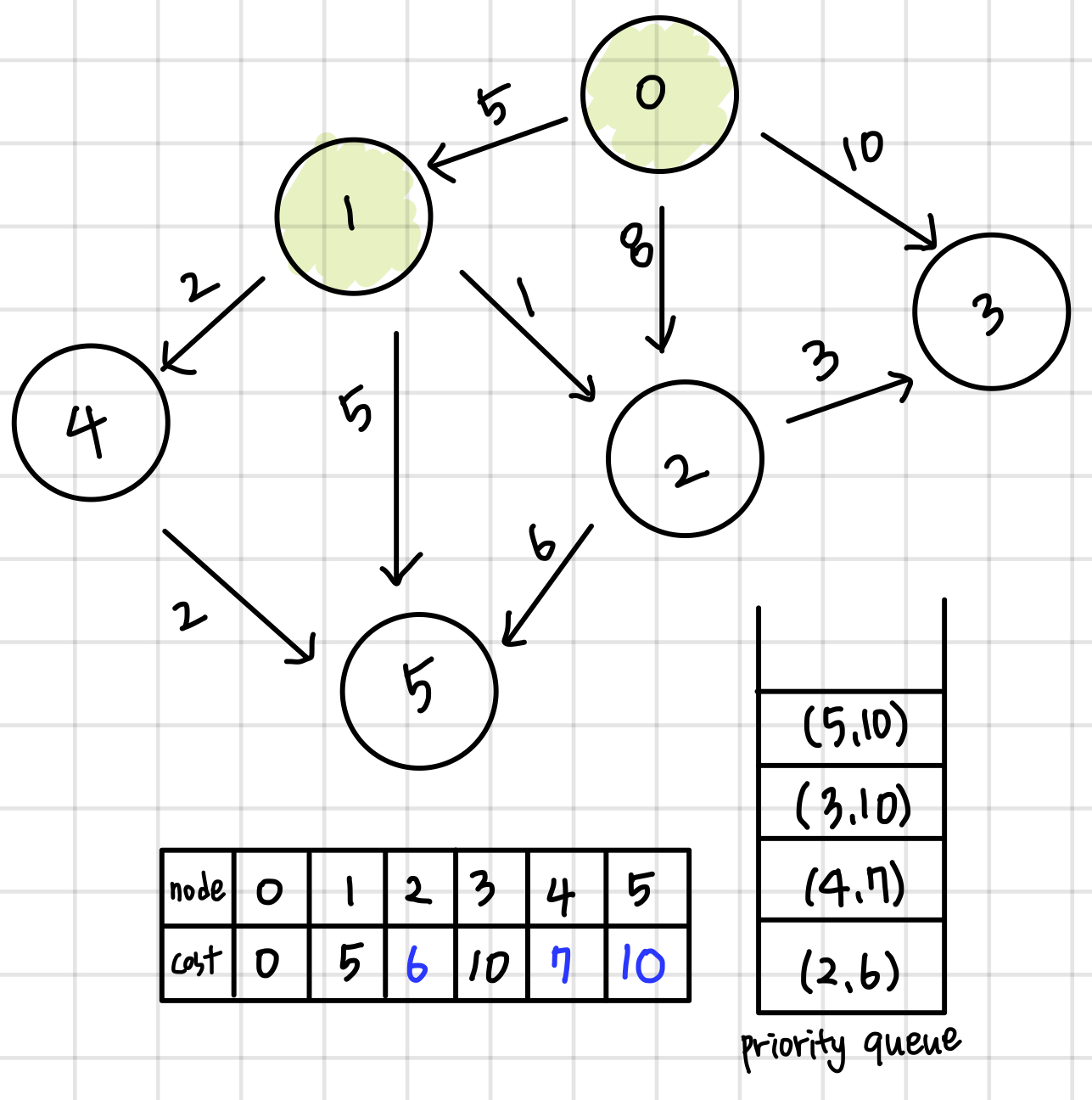
이전 과정과 동일한 과정을 priority queue가 빌때까지 반복한다.
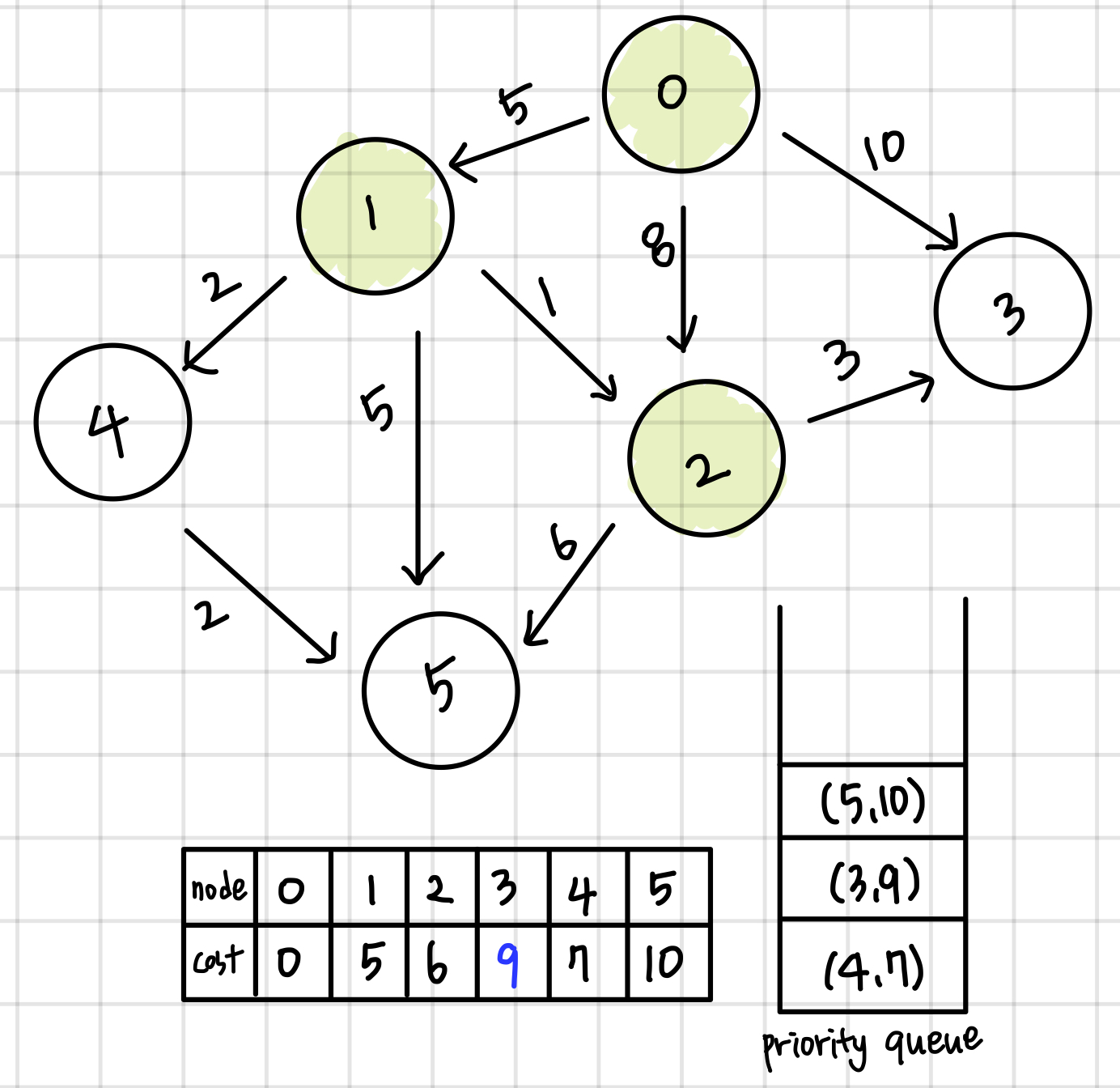
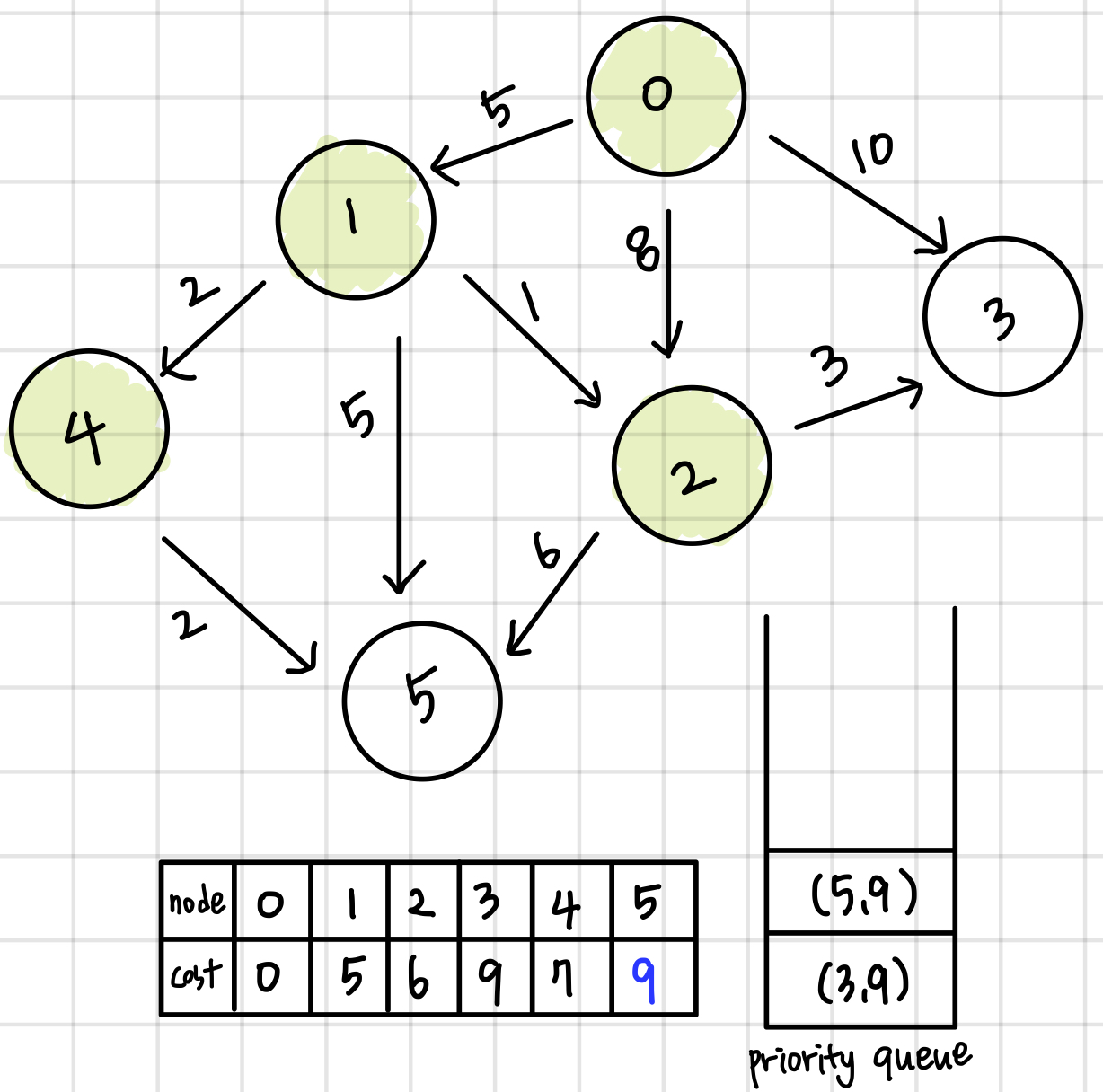
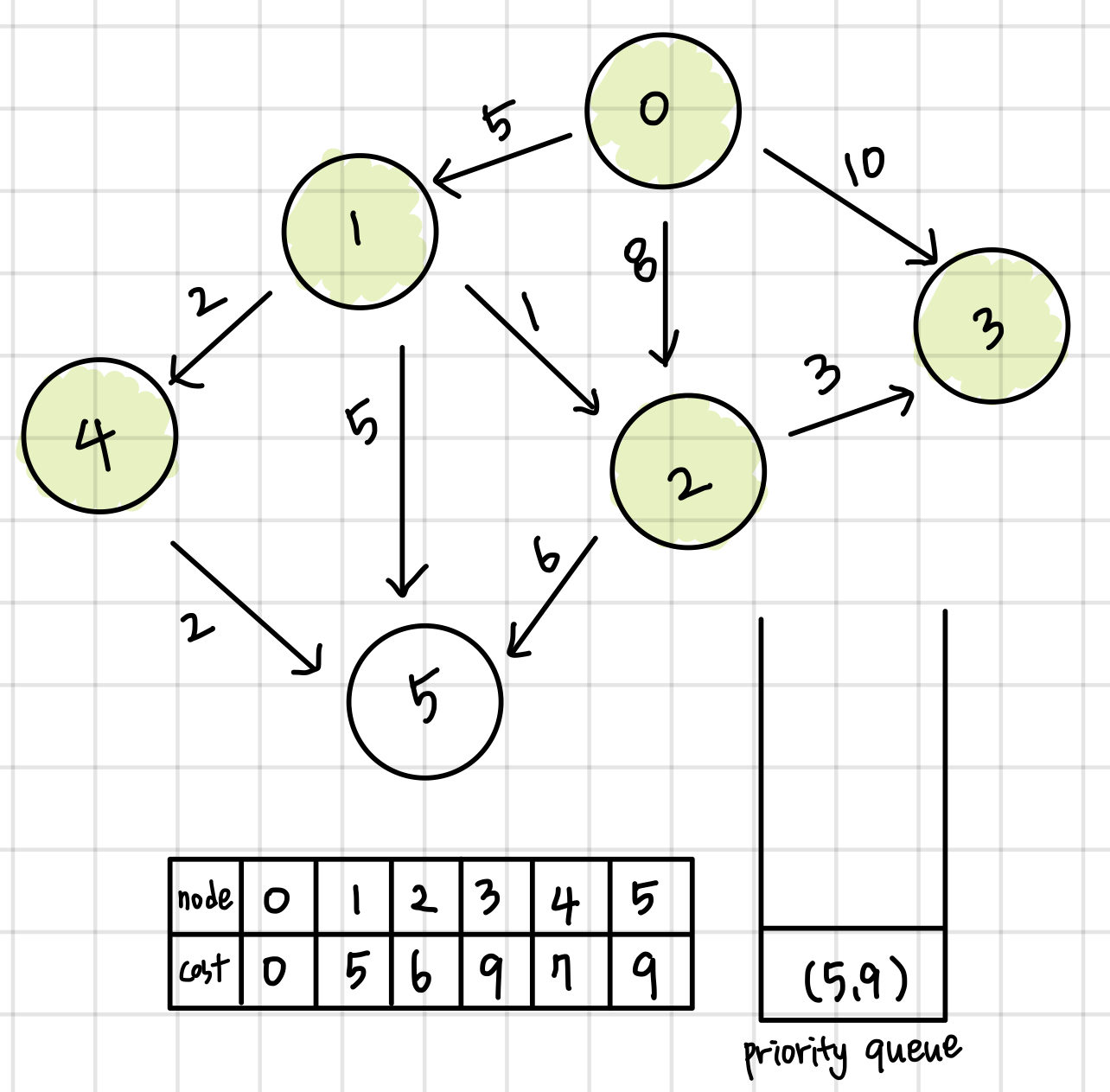
코드 (c++)
for (int i = 0; i < e; i++) {
int a, b, c;
cin >> a >> b >> c;
vec[a].push_back({ b,c });
}
for (int i = 1; i <= v; i++) {
minDis[i] = MAX_LEN;
}
minDis[k] = 0;
pq.push({ -minDis[k], k });
while (!pq.empty()) {
int node = pq.top().second;
int len = -pq.top().first;
pq.pop();
if(visited[node]) continue;
visited[node] = true;
for (int i = 0; i < vec[node].size(); i++) {
int nextNode = vec[node][i].first;
int nextEdge = vec[node][i].second;
if (len + nextEdge < minDis[nextNode]) {
minDis[nextNode] = len + nextEdge;
pq.push({ -(len + nextEdge), nextNode });
}
}
}
for (int i = 1; i <= v; i++) {
if (minDis[i] == MAX_LEN) {
cout << "INF\n";
}
else cout << minDis[i] << "\n";
}priority queue내에서 값이 오름차순으로 정렬될 수 있도록 음수로 값을 저장하였다. 양수로 사용하고 싶다면 priority queue를 정의할때 priority_queue<pair<int,int> ,vector<pair<int,int> >,greater<pair<int,int>> pq로 정의하면 된다.
예제
https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
'알고리즘 > 공부' 카테고리의 다른 글
| Javascript로 백준 풀기 (4) | 2023.03.13 |
|---|---|
| [알고리즘] 위상정렬(Topological Sort) (0) | 2022.01.11 |
| [알고리즘] 유니언 파인드(Union Find) (0) | 2022.01.10 |
| [알고리즘] 인덱스 트리(Indexed Tree) (1) | 2022.01.05 |
| [알고리즘] 그래프 (0) | 2021.09.20 |